TF*IDF and document similarity
What is TF*IDF and why do we need it?
TF*IDF, which stands for Term Frequency - Inverse document Frequency. Intuitively, a TF*IDF model tells us whether a specific term (or word) is important to identify a document among a collection of documents. Term frequency measures how often this term appear in one document and document frequency measures how often this term appear overall documents. When a word frequently appears in one document and not appears many in other documents, this specific word is very useful to identify this document. Assume we have 4 different documents:
Doc1. “Alice is a cute girl.”
Doc2. “Alice is a student.”
Doc3. “Bob and Alice are friends.”
Doc4. “Alice and Alice and Alice and Calvin”
Consider the term “Alice” and document 4. This term appear once in this document and twice overall documents. So the term frequency \(f_{(d,t)}\) = \(f_{(doc4,Alice)}\) = 3 and document frequency \(f_t\) = \(f_{Alice}\) = 6.
We can use a simple formula for calculation:
\(TF*IDF\ =\ f_{(d,t)}\ *\ \frac{1}{f_t}\)
So, \(TF*IDF_{(doc4,Alice)}\ =\ 1\ *\ \frac{3}{6}\ =\ \frac{1}{2}\).
The numeric value is quite small, which indicates that the term “Alice” may not be a good choice for identifying document 4. Let us try another term Calvin.
\(f_{(d,t)}\) = \(f_{(doc4,Calvin)}\ =\ 1\), \(f_t\) = \(f_{Calvin}\ =\ 1\)
\(TF*IDF_{(doc4,Calvin)}\ =\ 1\ *\ \frac{1}{1}\ =\ 1\).
Here the interesting thing comes. Although the term “Alice” appears 3 times more than the term “Calvin” in document 4, “Calvin” has a larger TF*IDF value. This is because Calvin only appear once overall documents, so if a document contains the term “Calvin”, it has to be document 4. Clearly, the term “Alice” has weaker identification ability than “Calvin”.
You can find a lot more about TF*IDF from wikipedia.
There are many different formulas for calculating TF*IDF, and they share the core of TF*IDF.
The classic TF*IDF formular: \(w_{(d,t)}\ =\ f_{(d,t)}\ *\ log\frac{N}{f_t}\)
Wait, what is \(w_{(d,t)}\) in that equation??
Vector Space Model for documents
Basically, a document can be represented as a vector:
\(<w_{(d,1)},w_{(d,2)},w_{(d,3)}......w_{(d,n)}>\)
\(w_{(d,t)}\) is a weight describing the importance of term \(t\) in document \(d\). TF*IDF is one way of determining this weight, another simple way is just the frequency of terms.
Similarity and Distance
With the vector space model, we can now use various ways to determine similarities or differences among documents.
Suppose we have two documents represented in vector space model:
A: \(<1,0,2,1>\)
B: \(<2,1,1,0>\)
Jaccard Similarity
\(Sim(A,B)\ =\ \frac{|A\cap B|}{|A\cup B|}\) = \(\frac{1+0+1+0}{2+1+2+1}\) = \(\frac{2}{6}\) = \(\frac{1}{3}\)
Notice that in the denominator, it is the count of all of words that occur in either sentence, and no double counting!
Dice similarity
\(Sim(A,B)\ =\ \frac{2|A\cap B|}{|A|+|B|}\) = \(\frac{2*2}{3+3}\) = \(\frac{4}{6}\) = \(\frac{2}{3}\)
Notice that in the denominator, we only care about occurence (Assume that A=<3,1,2,0>, |A| is still 3).
Cosine Similarity
\(Sim(A,B)\) = \(\frac{\vec a*\vec b}{|\vec a|*|\vec b|}\) = \(\frac{\sum_{i}a_ib_i}{\sqrt{\sum_{i}a_i}*\sqrt{\sum_{i}b_i}}\) = \(\frac{1*2+0*1+2*1+1*0}{\sqrt{1^2+0^2+1^2+0^2}\sqrt{2^2+1^2+1^2+0^2}}\) = \(\frac{2+0+2+0}{\sqrt{1+0+1+0}\sqrt{4+1+1+0}}\) = \(\frac{4}{\sqrt{2}\sqrt{5}}\) = \(\frac{2\sqrt{10}}{5}\)
 The bigger the cosine value is, the smaller the angle between the two compared vectors is and thus the two vectors are more similar.
The bigger the cosine value is, the smaller the angle between the two compared vectors is and thus the two vectors are more similar.
Manhattan Distance (L1 distance)
\(d(A,B)\) = \(\sum_{i=1}^{n}|a_i-b_i|\) = \((1-2)^2+(0-1)^2+(2-1)^2+(1-0)^2\) = \(4\)
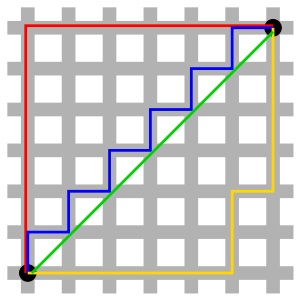
Euclidean Distance (L2 distance)
\(d(A,B)\) = \(\sqrt{\sum_{i=1}^{n}(a_i-b_i)^2}\) = \(\sqrt{(1-2)^2+(0-1)^2+(2-1)^2+(1-0)^2}\) = \(\sqrt{1+1+1+1}\) = \(2\)